【深度学习】用于Transformer的FLOATER位置编码

2023-05-15 PV:

由于博客排版有误，欢迎移至知乎阅读：https://zhuanlan.zhihu.com/p/629476200

0x00 来源论文

Learning to Encode Position for Transformer with Continuous Dynamical Model

0x01 引言

位置编码（Positional Encoding）是 Transformer 模型的预处理的一个重要部分。之所以引入位置编码，是为了解决自注意力机制（Self-attention）中没有办法区分输入向量之间距离的问题。具体来说，如果我们要处理 I love you. 这么一个句子，在没有位置编码的情况下，Transformer 架构会认为 I love 的距离和 I you 是一样的。总而言之，在自注意力机制里面，根本就没有位置的信息，但是实际上位置的信息有的时候是很重要的，因此位置编码机制应运而生。位置编码机制千奇百怪，而在上述论文中，它提出了一种叫作 FLOATER 的位置编码，这将是我们在这篇博客中讲解的重点。

0x02 位置编码

让我们先来回顾一下位置编码具体是怎么操作的。假设在 Transformer 架构中，有一个输入向量 $a^i$，那么由它分别左乘三个矩阵 $W^q,W^k,W^v$ 得到 $q^i,k^i,v^i$，它们分别表示 $a^i$ 的 query、key 以及 value。那么 $a^i$ 对应的注意力值就是：
$$
\alpha^i=[k^1,k^2,k^3,\dots,k^L]^\top q^i
$$
一般来说我们会对 $\alpha^i$ 作 $\rm softmax$ 操作，即 $\alpha{^\prime}^i=\mathop{\rm softmax}(\alpha^i)$。这样我们就得到了自注意力。

正如前文所说，我们需要引入一个位置编码。而这个位置编码是和输入同大小的一串向量，比如对于 $a^i$ 就有一个对应的位置编码 $e^i$，这时我们就把 $a^i+e^i$ 作为输入向量。即：
$$
q^i=W^q(a^i+e^i)
$$
$$
k^i=W^k(a^i+e^i)
$$
$$
v^i=W^v(a^i+e^i)
$$
这看起来很简单，但实际上这个 $e^i$ 是需要由我们手动来设定一个生成规则的（虽然现在已经有人提出把它也作为可学习参数进入网络，但是至少最开始的时候是手工的）。其中比较著名的有 Sinusoidal、Position embedding 以及 RNN 生成，当然不要忘了这篇文章中提出的 FLOATER。它们分别长这样：

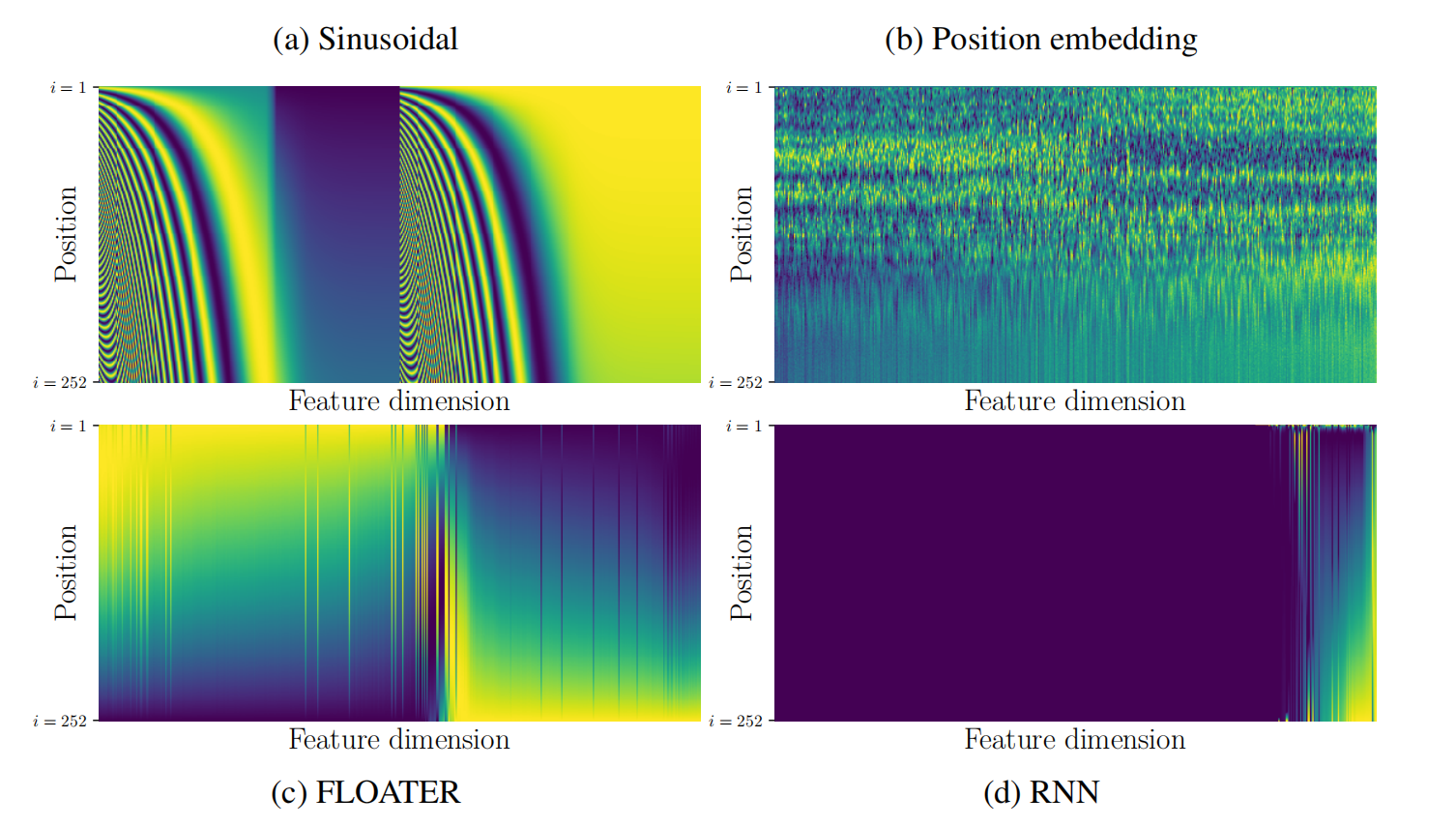
其中，越深色代表越接近-1，越浅色代表越接近1。

这篇论文同时也对比了一下这几种方法：

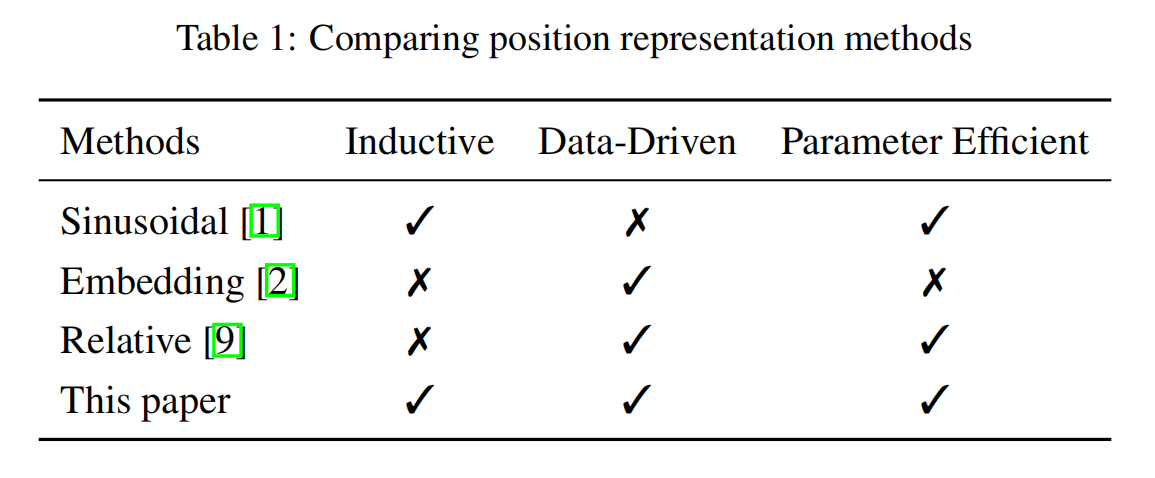
可以看到，它所提出的 FLOATER 还是非常优秀的。

0x03 FLOATER

接下来进入正题，介绍一下FLOATER。

FLOATER 全称 FLOw-bAsed TransformER（事实上在这篇论文里面你可以看到 FLOWER 和 FLOATER 两种表述，它们是一种东西，只是取了不同的首字母而已，不是很清楚为什么论文作者们没有统一一个名称），它的主要思想是将位置编码建模为连续动态系统（Continuous Dynamical System），因此只需要学习系统动态而不是独立地学习每个位置的嵌入向量 $e^i$。

所谓连续动态系统，它描述了在连续时间内，系统的状态如何随时间变化而变化。这种系统通常用微分方程来描述，其中系统的状态在任意时刻都由状态变量和它们的导数（即状态变量随时间的变化率）来表示。

为了使网络能够通过反向传播进行训练，这篇论文采用了神经常微分方程（Neural ODE），即自由形式流模型（Free-form Flow Model）。

0x03-1 动态系统位置编码

这里我们统一将符号改为和论文中的一致。位置编码是一个向量序列 ${p^i\in \mathbb{R}^d:i=1,\dots,L}$，输入向量 ${x^i\in\mathbb{R}^d:i=1,\dots,L}$。

既然采用了动态系统的架构，那么我们认为有一个潜在力（latent force），记为 $h^i$，是它把将 $p^i$ 转移到了 $p^{i+1}$。

那么假设函数 $p(t)$ 是 ${p^i}$ 的连续光滑版本，我们的动态系统应该满足：
$$
p(t)=p(s)+\int_s^th(\tau,p(\tau);\theta_h){\rm d}\tau,0\le s\le t<\infty
$$
其中，$h(\tau,p(\tau);\theta_h)$ 代表参数 $\theta_h$ 和前一时刻状态 $(\tau,p(\tau))$ 构成的神经网络。

既然 ${p^i}$ 是离散的而 $p(\cdot)$ 是连续的，我们可以取 ${t^i=i\cdot\Delta t}:p^i=p(t^i)$，其中这个 $\Delta$ 是一个超参数，论文里设置的是 $\Delta=0.1$。

不难看出，上面的由 $p(s)$ 到 $p(t)$ 的转移方程实际上可以表达成一个常微分方程问题：
$$
\dfrac{\mathrm{d}p(t)}{\mathrm{d}t}=h(t,p(t);\theta_h)
$$
为了训练网络，在反向传播过程，我们需要求解损失函数 $L(p^0,\dots,p^L)$ 关于 $\theta_h$ 的梯度。我们有：
$$
\dfrac{\mathrm{d}L}{\mathrm{d}\theta_h}=-\int_t^s a(\tau)^\top\dfrac{\partial h(\tau,p_\tau;\theta_h)}{\partial\theta_h}\mathrm{d}\tau
$$
其中 $a(\tau)$ 是常微分方程的伴随状态，可以由另一个常微分方程计算：
$$
\dfrac{\mathrm{d}a(\tau)}{\mathrm{d}\tau}=-a(\tau)^\top\dfrac{\partial h(\tau,p_\tau;\theta_h)}{\partial p_\tau}
$$
在后面我们会讲到如何设置常微分方程的自动求解器。

0x03-2 块间参数共享

我们知道，在 seq2seq Transformer 的架构中一共有6个块，BERT 有12或24个块，我们可以尝试在每一个块都进行位置编码来优化网络的性能。但是同时拥有 $N$ 个不同的动态系统 $h^{n}(\cdot;\theta_h^n)$ 会引入很多参数，这样的话训练开销会很大。因此，我们令：
$$
\theta_h^1=\theta_h^2=\dots=\theta_h^N
$$

0x03-3 对原始 Transformer 的兼容性

实际上，FLOATER 和原始的 Transformer 模型是兼容的。我们考虑正弦式编码（sinusoidal encoding）：
$$
\tilde{q}^i=W^q(x^i+\tilde{p}^i)+b^q
$$
这个公式的意思是，一个输入向量的 query 值是 $\tilde{q}^i$ 是由模型参数 $W^q,b^q$ 以及它本身 $x^i$ 和位置编码 $\tilde{p}^i$ 计算而来的。$\tilde{k}^i,\tilde{v}^i$ 以此类推，不赘述。

假如引入的是 FLOATER 模型，那么就有：
$$
q^i=W^q(x^i+p^i)+b^q
$$
$$
=W^q(x^i+\tilde{p}^i)+b^q+W^q(p^i-\tilde{p}^i)
$$
$$
=\tilde{q}^i+b^{q,i}
$$
可以看到，从正弦式编码到 FLOATER 本质上就是把原来的偏置 $b^q$ 改成了一个考虑位置 $i$ 的新偏置 $b^{q,i}$。因此，我们就有了这样的动态系统：
$$
b^q(t)=b^q(0)+\int_0^th(\tau,b^q(\tau);\theta_h)\mathrm{d}\tau
$$
在此基础上，我们令 $b^{q,i}=b^q(i\cdot\Delta t)$。而当 $h(\cdot)=0,b^q(0)=0$ 时，有 $q^i=\tilde{q}^i$，即 FLOATER 退化为了正弦式编码。

因此，利用这种兼容性，我们可以直接用预训练的 Transformer 模型初始化 FLOATER 模型，然后在下游任务进行微调。而对于类似 BERT 或 Transformer-XL 之类的模型，我们已经为下游任务提供了 checkpoint。为了对比 FLOATER 模型和其他模型的表现，论文中逐层复制了注意力和 FFN 层的权重，并随机初始化了 $h(\tau,p(\tau);\theta_h)$。

0x04 实现及实验结果

论文把 FLOATER 放在了一些 NLP 任务中进行测试并与其他模型进行了比较。

0x04-1 设置常微分方程自动求解器

论文用的常微分方程求解器是经过修改的 torchdiffeq 库，可以在此链接下载。

神经机器翻译任务上，采用步长 $\dfrac{\Delta}{5.0}$（前面设置了 $\Delta=0.1$）的 Runge-Kutta 法（即通过计算在每个时间步长之间各个中间点的解斜率的加权平均数来近似计算ODE的解），在 GLUE 和 RACE 上测试。

0x04-2 神经机器翻译任务

论文运行了由 fairseq 提供的预处理脚本成功复现了 Transformer 论文 Attention is all you need 中的所有结果，然后按照下面的步骤获得了这篇论文的结果：

对原始 Transformer 模型进行30个 epoch 的训练；
随机初始化 FLOATER 模型；
从验证集里表现最佳的 checkpoint 初始化 FLOATER 模型，同时给动态模型里的权重 $\theta_h$ 赋一个比较小的值；
将峰值学习率减半；
使用预处理好的 FLOATER checkpoint，在相同的数据集上进行10个 epoch 的英德翻译训练和1个epoch 的英法翻译训练；
对最后5个 checkpoint 取平均，并在测试集上计算 BLEU 分数。

以下是实验结果：

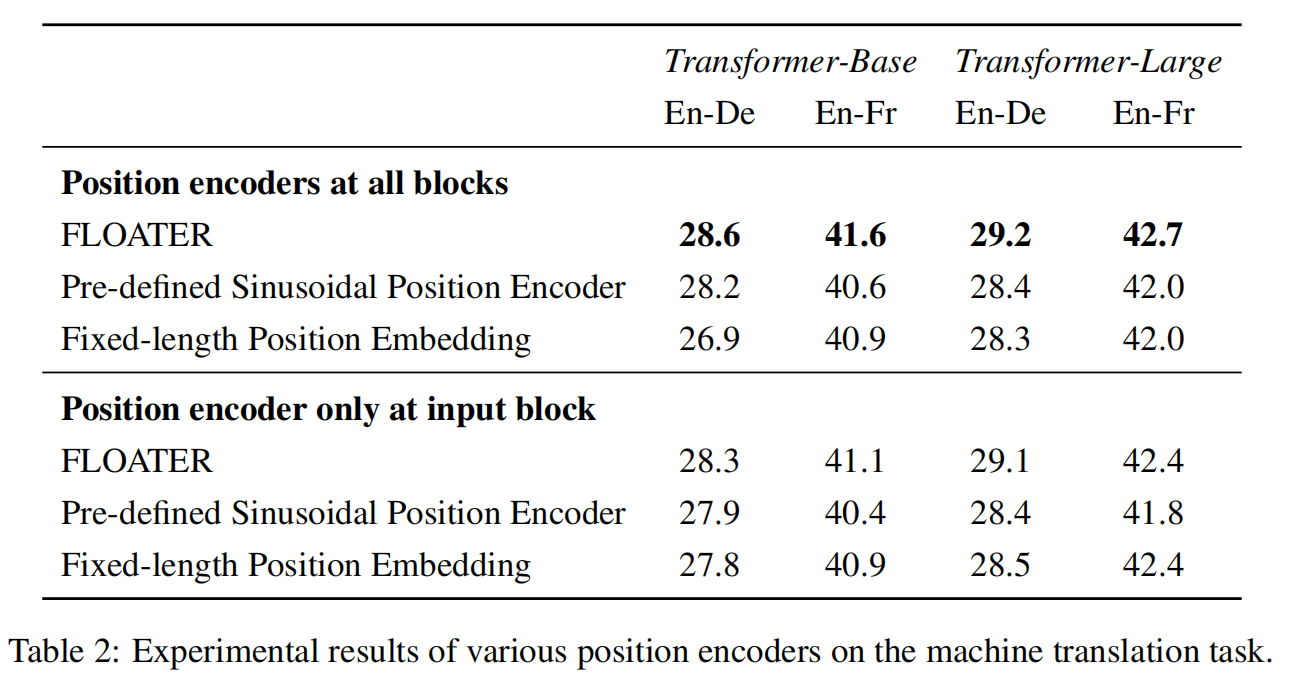
0x04-3 语言理解任务

对于 GLUE/SQuAD/RACE 基准测试，论文中的实验都是基于 RoBERTa 进行的，包括 base 和 large 两种配置。由于资源限制，使用的是预训练的 RoBERTa 来初始化 FLOATER 模型，类似于神经机器翻译任务。但是由于 GLUE/SQuAD/RACE 数据集过小，无法从头开始训练，因此动态系统动态函数 $h(\tau,p(\tau);\theta_h)$ 的权重 $\theta_h$ 是在 WikiText103 数据上使用 Masked Language Modeling Loss 进行预训练的，而且只训练 $\theta_h$。所谓 Masked Language Modeling Loss，指的是输入的文本序列中的一些词语被随机遮蔽，模型需要预测这些遮蔽词语的正确词汇。这可以让模型学会从上下文中推断出遮蔽掉的词语，从而提高模型对于语言的理解和生成能力。论文发现单独训练 $\theta_h$ 时，只需要几个小时（配置是2个 Titan V100）和一个训练周期就可以达到收敛。

GLUE 基准：8个数据集和不同的超参数设定。论文使用的是和 RoBERTa 中一样的超参数。

SQuAD 基准（来源1 和来源2）：论文自己写了微调代码，同样使用的是 RoBERTa 里面的超参数。

RACE 基准：有最长的上下文和序列长度。使用 RoBERTa 里的超参数。冻结权重 $\theta_h$，并且只微调 RoBERTa 的权重。

以下是实验结果：

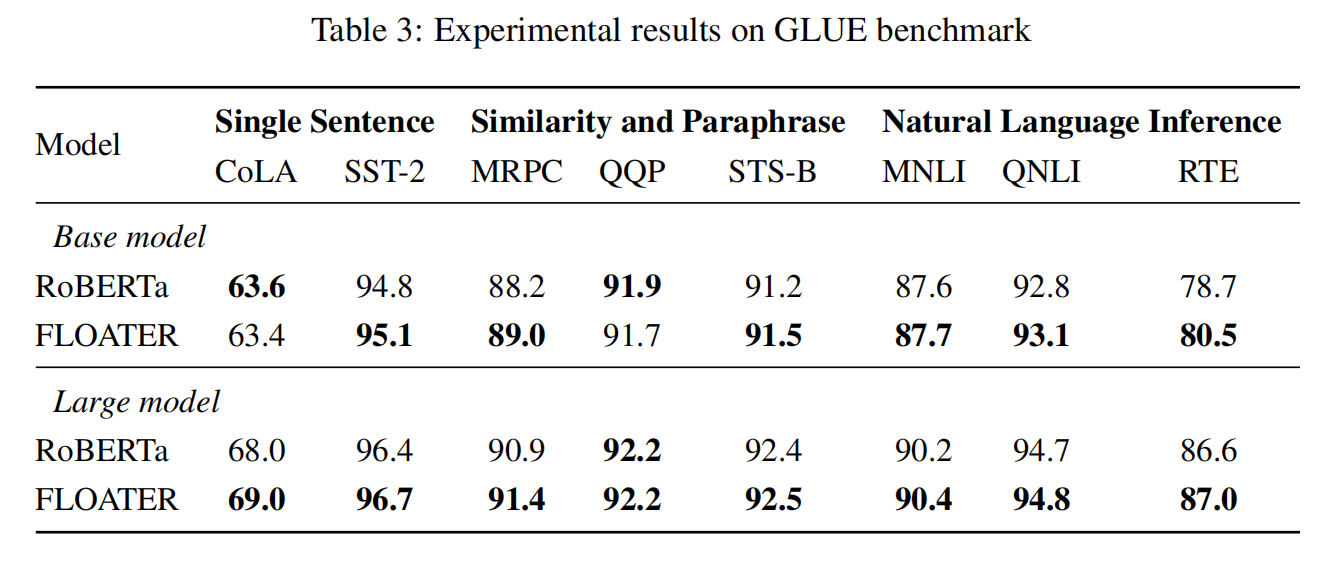
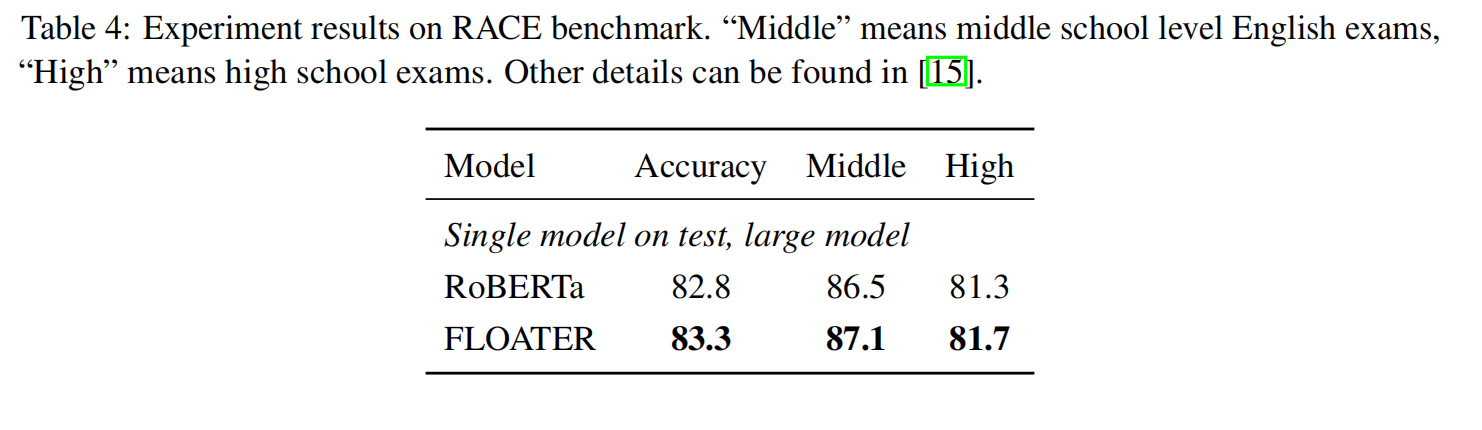
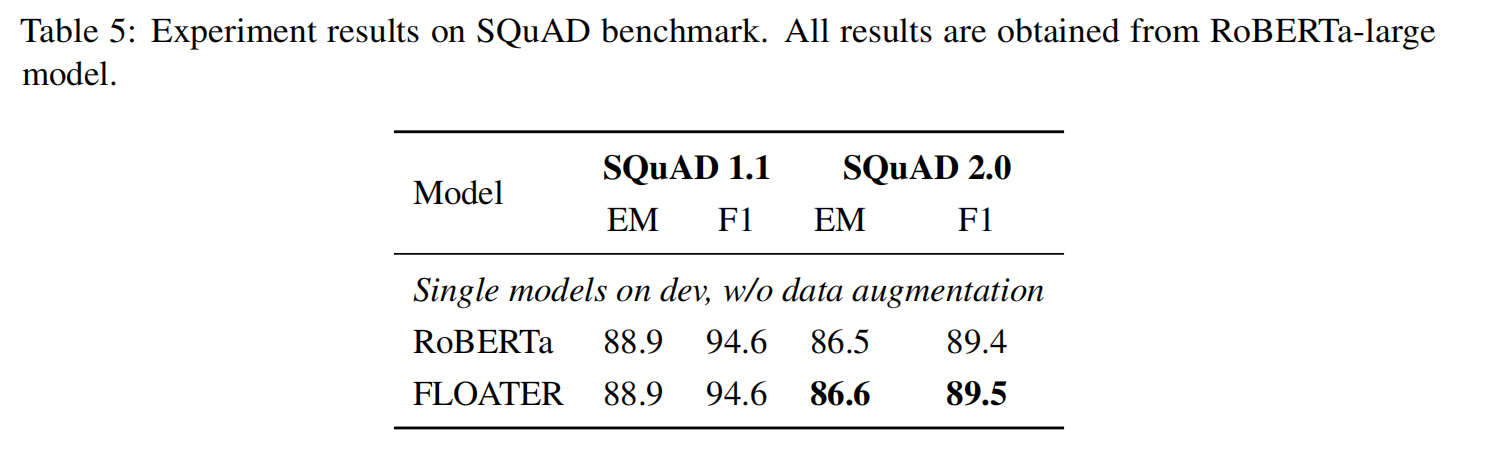
0x05 讨论与分析

0x05-1 泛化能力

论文作者们注意到在 WMT14 英德数据集上有98.6%的训练句少于80个 tokens，所以他们做了一个新的数据集，En-De short to long，简称 S2L，即把小于80个 tokens 的句子作为训练集，其余的作为测试集，而又进一步将测试集根据 tokens 数量分为4个部分：$[80,100),[100,120),[120,140),[140,+\infty)$，计算出来的 BLEU 分数如下：

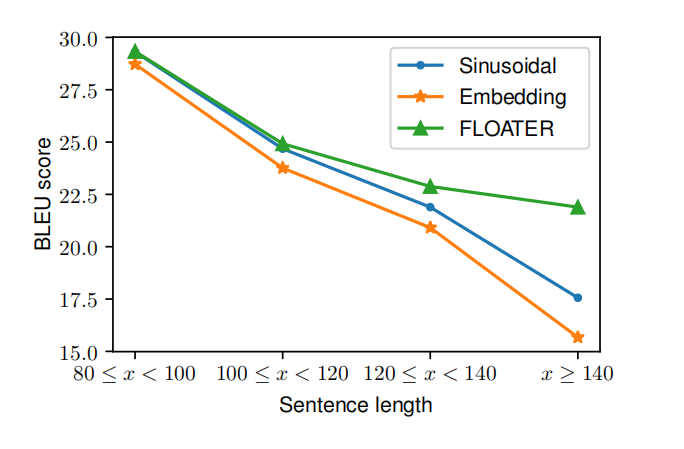
可以看出，FLOATER 的泛化能力非常优秀，即便是训练集只提供短句子，也能够适用于长句子。

0x05-2 与 RNN 的比较

众所周知，RNN 也可以用于序列模型，而且和 FLOATER 一样，第 $i$ 步也是依赖于第 $(i-1)$ 步的。论文就将 RNN 与 FLOATER 的性能进行了对比。
$$
p^{i+1}=\mathrm{RNN}(z^i,p^i)
$$
其中 $p^i$ 是之前提到的位置编码，$z^i$ 是 $i$ 处 RNN 的输入。实验结果如下：

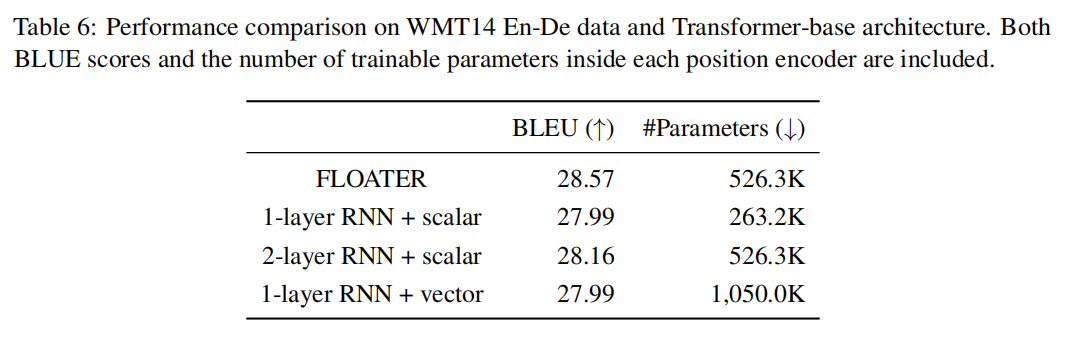
0x05-3 训练与测试效率

由于利用流模型求解神经常微分方程一次需要大概100次前向和反向传播，再加上常微分方程求解器无法利用 GPU 并行运算的优势，FLOATER 模型的开销是非常大的。论文提出了以下几种方法来改进：

利用已经训练好的模型来初始化；
用较小的数值初始化 FLOATER；
因为 $h(\cdot)$ 训练起来比较容易和稳定，可以将它与网络的其他部分分离出来；
对于 RoBERTa 模型，直接下载预训练的模型，插入 FLOATER 编码层，然后重新训练编码层；而在 GLUE 上微调时，直接冻结编码层使它不变。

利用上述方法，FLOATER 只花了比 Transformer 多20-30%的时间来训练。

0x06 总结与展望

这篇论文将 Neural ODE 和 Transformer 结合起来提出了 FLOATER 模型，并取得了较好的效果。但是自然语言的高度离散化让连续性假设可能不再实用，而且 Neural ODE 仍处于发展阶段，没有得到广泛的应用。而且 TENER 指出本文（以及其他传统模型）将位置编码和输入向量相加的方式会导致位置编码在后续变换中消失。

0x07 参考文献

[1] Learning to Encode Position for Transformer with Continuous Dynamical Model: https://arxiv.org/abs/2003.09229

[2] TENER: Adapting Transformer Encoder for Named Entity Recognition: https://arxiv.org/abs/1911.04474